Backpropagation 란 무엇인가?
오랜만에 네이버 블로그에 작성해 둔 글들을 다시 연재합니다. 지난 글들을 보니 제가 쓴 글이지만 허접(?)하네요. 그래도 유익하길 바라며, 많은 피드백 부탁드립니다.
들어가며
다음은 신경망 성능을 결정하는 요소들입니다.
- 컴퓨터 성능(고성능 GPU, 돈이 필요하네요…)
- 대량의 고품질 학습 데이터 (이것도 다 돈이죠…)
- 학습 알고리듬
이들 중 덜 중요한 것은 없습니다. 세가지 요소가 들어맞을 때 제대로된 딥러닝 서비스가 가능하죠. 컴퓨터 성능이나 학습 데이터와 같은 외부 요소는 논외로 하고, 우선 소프트웨어적으로 주어진 데이터를 더 빠르고 제대로 학습하는 방법, 즉 학습 알고리즘에 대해서 다루고자합니다. 그리고 그 가운데에서도 신경망 학습 알고리즘의 근원이 되는 역전파(이하 Backpropagation)**를 알고자합니다.
본문
1986년, 제가 기어다닐 시기에…, 제프리 힌튼(G. Hinton) 교수는 신경망 연구에서 획기적인 성과를 발표합니다. 바로 Backpropagation 알고리즘 입니다. 신경망의 출력값과 기대값 사이의 오차를 최소화 시키는 방향으로 각 연결들의 가중치를 조잘하는 방법이죠. 이러한 연결 가중치의 갱신 과정이 출력층에서 입력층으로 역방향으로 이루어지기에 Back-propagation이라고 합니다.
Backpropagation의 원리를 이해하는 것은 수식을 통해서 파악하는 것이 가장 올바른 방법이라고 생각합니다. 쉬운 설명을 위해서 2개의 층으로 이루어진 단순한 신경망을 사용하겠습니다. 실제 딥러닝에서 사용되는 신경망들은 훨씬 복잡한 구조를 이루지만, 학습 방법의 뿌리가 Backpropagation라는 점은 공통적입니다.
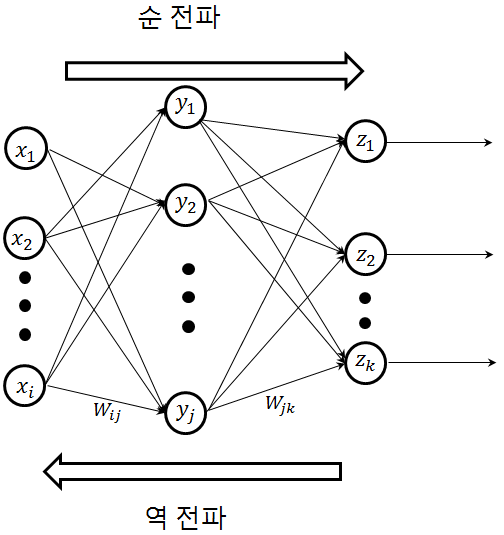
Backpropagation은 신경망 학습에서 층과 층사이 존재하는 연결들에 대한 최적의 가중치를 찾는 과정입니다. 최적의 가중치는 어떻게 찾는걸까요? 그건 바로 최적화 문제로 접근하는 것입니다. 신경망에서 출력된 값과 기대한 값 사이의 오차를 비용함수(이하 Cost Function)로 두고, 이 함수 값이 최소가 되도록 하는 함수 파라미터 값(=연결 가중치 값)을 찾는것이죠.
이러한 Cost Function이 최소(지역적 최소)가 되도록 함수 파라미터들을 조절하는 데는 경사 하강법(이하 Gradient Descent)을 사용합니다. 가령, 깊은 밤 지도가 없는 상황에서 산 중턱에 남겨졌다고 할 때, 가장 빨리 마을을 찾는 방법이 무엇일까요? 아마도 현 위치에서 급경사를 타고 내려가는 것이겠죠. Gradient Descent도 Cost Function를 그래프로 표혔했을 때, 현 위치에서 가장 기울기가 낮은 방향으로 파라미터 값을 이동시키고 평탄한 지점에 도달할 때까지 이 행위를 반복하는 것입니다.
이제 Backpropagation과정을 살펴보겠습니다. 우선 간단한 전제를 두겠습니다.
- 활성화 함수로는 시그모이드를 사용합니다. (논문이 발표된 이래로 가장 많이 사용된 활성화 함수죠.)
-
기대값과 출력값 사이의 오차를 의미하는 Cost Function은 크로스엔트로피 식를 사용합니다.
Backpropagation은 크게 아래 세 단계로 이루어집니다.
-
순-전파 : 학습 데이터로부터 출력값\(Z_i\)과 기대값\(t_i\)의 오차 구하기
-
역-전파 : 출력층에서 입력층 방향으로, 오차에 대한 각 연결 별 기여도 계산하고, 이 기여도만큼 기존 연결 가중치에서 삭감.
-
오차에 대한 전체 연결들의 영향도가 0에 수렴할 때 까지, 또는 그전에 사용자가 지정한 제약조건에 도달할 때까지 1~2를 반복.
우선, 순-전파(Feed-Foward) 부분입니다.
“학습데이터로 부터 출력된 값과 기대한 값의 오차”는 다음 크로스 엔트로피식으로 정의합니다. \(E = -\sum_{i=1}(t_i\log(Z_i)+(1-t_i)\log(1-Z_i))\)
다음으로, 역-전파(Feed-Backward) 부분입니다.
오차 \(E\)에 대하여, 출력층\({Z}_{i}\)과 그 직전층\({Y}_{j}\)사이의 특정 연결 \({W}_{ji}\)가 기여도는 미분을 사용하고, 아래와 같이 정의됩니다.
\(\frac{\partial E}{\partial {W}_{ji}}\)
위 미분은 다음과 같이 유도가 가능합니다.
\(\frac{\partial E}{\partial W_{ji}}=\frac{\partial E}{\partial Z_{i}}\frac{\partial Z_i}{\partial S_i}\frac{\partial S_i}{\partial W_{ji}}\)
우항의 각 부분을 전개하면 다음과 같습니다.
\(\frac{\partial E}{\partial Z_i}=\frac{\partial(-\sum_{i=1}(t_i\log(Z_i)+(1-t_i)\log(1-Z_i)))}{\partial Z_i}=\frac{-t_i}{Z_i}+\frac{1-t_i}{1-Z_i}=\frac{Z_i-t_i}{Z_i(1-Z_i)}
\\
\frac{\partial Z_i}{\partial S_i}=\frac{\partial (\frac{1}{1+e^{-{S}_{i}}})}{\partial S_i}={Z_i}{(1-Z_i)}
\\
\frac{\partial S_i}{\partial W_{ji}}=Y_j\)
이제 연결 \({W}_{ji}\의 가중치를 조정하는 식을 볼까요? 아래가 갱신된 가중치를 구하는 식입니다. \(\alpha\)는 사용자가 지정하는 학습률 파라미터입니다.
\[W_{ji}={W}_{ji}-\alpha{\frac{\partial E}{\partial {W}_{ji}}}\]이 식을 해석하면 현재 연결 가중치에서 오차에 기여한 만큼을 감한다는 것을 의미합니다. 이러한 조정을 통해 오차를 점차 최소화 시켜나가죠.
그래디언트 소실 문제(Vanishing Gradient Problem)
당대에 획기적이었던 Backpropagation도 완벽한 알고리즘은 아니었습니다. 신경망의 층이 깊어질수록 학습 시간이 너무 오래걸리거나 학습 데이터에 지나치게 오버피팅(over-fitting)하는 문제가 발견된 것이죠. 가장 큰 원인으로 그래디언트 소실 문제(이하 Vanishing Gradient Problem)가 지목되었고, 이 문제가 바로 해결되지 않아 1986년부터 2006년까지 신경망 연구분야에 침체기가 있었습니다.
사실 Vanishing Gradient Problem은신경망에서 사용한 시그모이드라는 활성화 함수 때문에 발생하였습니다. Backpropagation이 제안된 당시만 하더라도 활성화 함수로 시그모이드와 Tanh 함수를 사용하고 있었죠.
시그모이드 함수(아래 그림 좌)는 non-linear이면서 모든 실수 세계의 값을 0과 1사이로 압축시켜주는 녀석이죠. 하지만 시그모이드 함수의 미분상태(아래 그림 우)를 보면 입력값이 0 주변인 경우를 제외하고는 대부분은 미분값이 0에 가까운 값들을 가집니다. 이러한 특성때문에 신경망의 층이 깊어질 수록 Backpropagation 학습 알고리즘을 적용했을 때, 출력층에서 입력층으로 가는 과정에서 체인룰에 의해서 시그모이드 함수의 미분값이 중첩됨에 따라 입력층에 가까워지게 되면 거의 미미한 수준까지 가게 되죠. 이 때문에 연결 가중치에 대한 갱신이 제대로 발생하지 않아 최종적으로는 학습이 제대로 이루어지지 못한 상태가 발생하게 됩니다.
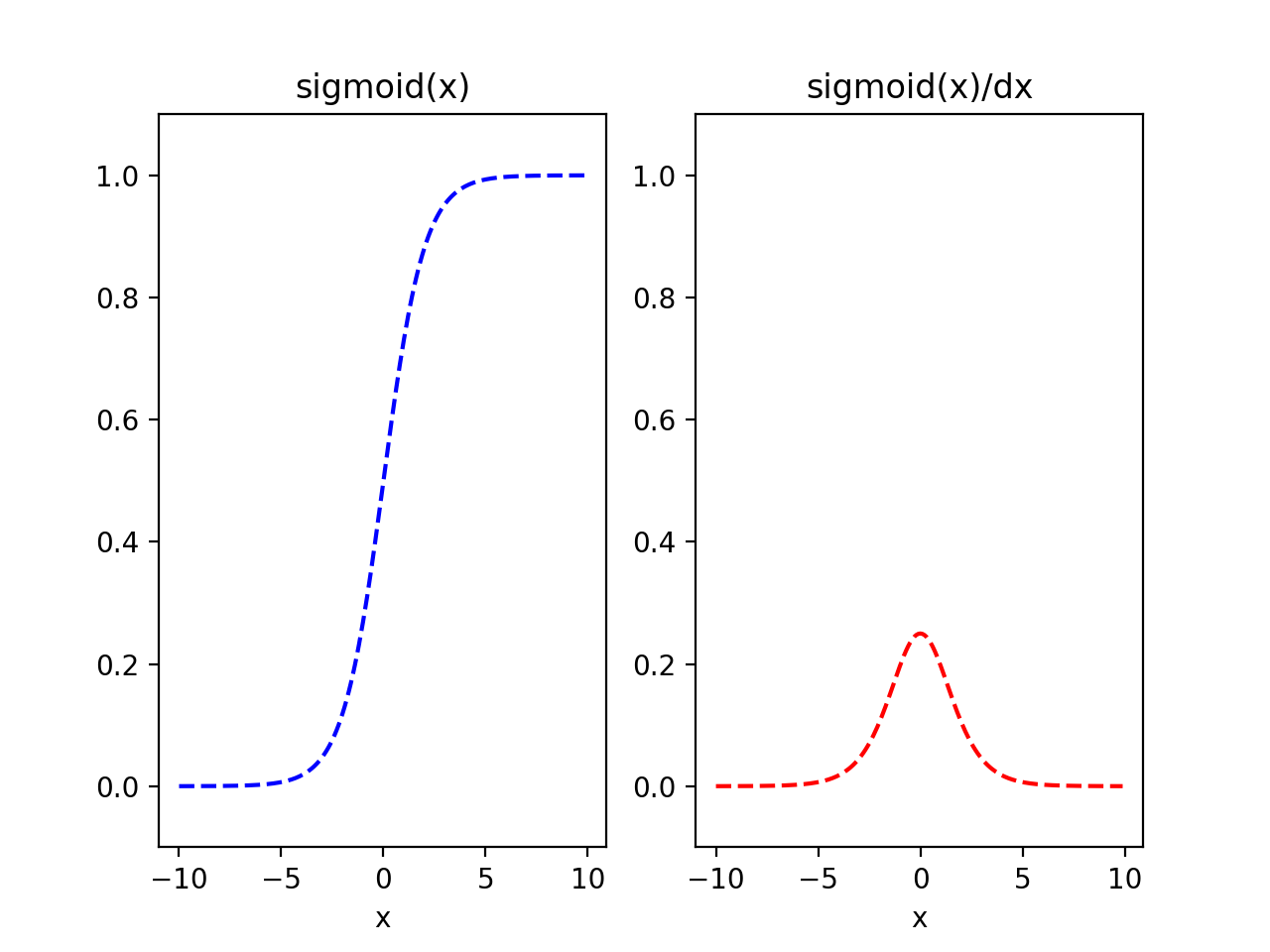
그나마 출력층에서는 괜찮은데, 왜 입력층으로 갈 수록 연결 가중치에 대한 업데이트가 제대로 이루어지지 않는 걸까요? 수식으로 한번 보겠습니다.